金氏運動公司打算舉辦一場馬拉松比賽,為了締造亮眼的完成比賽時間,金氏運動公司打算選擇性地邀請選手參賽。分析過往的數據資料,金氏運動公司觀察到以下二個現象:
(a) 對於任何一位選手,如果愈多他的朋友參賽,則他就能跑得愈快,所以傾向於找一群選手使得彼此互相認識的情況很多。因為認識是雙向的,如果$P$認識$Q$,則$Q$認識$P$。所以當我們說$P$認識$Q$時,等同於表示$P$、$Q$兩位互相認識。
(b) 如果參賽的選手當中,存在兩位選手$P$和$Q$彼此不認識,而且在參賽的選手當中無法找到$t$位選手$S_1,S_2,…S_t$($t$為任意大於0的整數),使得$P$認識$S_1$,$S_2$認識$S_3$,…,$S_{t-1}$認識$S_t$,$S_t$認識$Q$,則比賽將會有嚴重的惡性競爭,所以需要避免這樣的狀況。
現在金氏運動公司手上有一份$N$位選手的名單以及一份顯示這$N$位選手彼此之間是否認識的表單,現在的任務是從這$N$位選手找出選手的子集合$S = {P_1, P_2, \ldots, P_{\lvert S \rvert} }$,使得$S$沒有惡性競爭的狀況,而且讓以下影響因子$F(S)$得到最大化,這影響因子的設計除了讓每位選手都認識夠多的參賽者,也兼顧了不讓參賽人數過少。
$$F(S)=|S|\min_{1\le i\le |S|}D_i$$
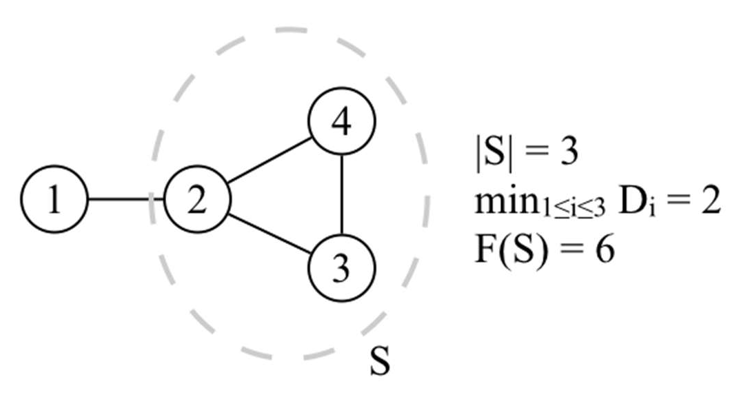
其中$D_i$表示選手$P_i$所認識的人當中,有多少人在子集合$S$裡面。在以下這個4位選手的例子中,選$S = {2, 3, 4}$比其他的選法有更高的$F(S)$。
$N\le 5000, M\le \frac{N\times (N-1)}{2}$
這題簡單來說就是選取一個連通子集,且她們的最小度數*子集大小最大。
考慮枚舉最小的度數$D$由小到大,不斷將度數小於最小度數的點都拔掉,同時檢查她周遭的點是否會因為這個點被拔而跟著被拔。可以用bfs配合求拓樸排序那種手法處理,然而在找連通塊大小時得做一次dfs,總複雜度會退化成$O(N(N+M))$(當然,可以直接砸可反悔的dsu)。
既然沒辦法好好維護連通塊大小,那就改成枚舉大到小,不斷把度數大於等於最小度數的都加進圖,直接用dsu維護最大連通大小,不過會遇到一個問題:該怎麼判斷加點的順序。
這就是這題有趣之處:事實上,直接將拔點順序反著插入會是好的。
詳細證明我也不會,大概就是拔點都是拔整個會影響的連通塊,插入也自然是插入整個連通塊。
所以就把拔點順序加進一個stack就好了
複雜度$O(N^2+M)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
|
#include <bits/stdc++.h>
using namespace std;
#define EmiliaMyWife ios::sync_with_stdio(0); cin.tie(NULL);
const int N = 1e4;
int pa[N], sz[N];
int fnd(int x) { return pa[x] == x ? pa[x] : pa[x] = fnd(pa[x]); }
void uni(int a, int b) {
if((a = fnd(a)) == (b = fnd(b)))
return;
if(sz[a] > sz[b])
swap(a, b);
sz[b] += sz[a];
pa[a] = b;
}
signed main() {
EmiliaMyWife
int n, m, ans = 0;
cin >> n >> m;
for(int i = 1; i <= n; i++)
pa[i] = i, sz[i] = 1;
vector<vector<int>> edge(n + 1);
vector<int> cnt(n + 1), rcnt(n + 1), has(n + 1);
for(int i = 0, a, b; i < m; i++)
cin >> a >> b, cnt[a]++, cnt[b]++, edge[a].push_back(b), edge[b].push_back(a);
stack<int> owo;
for(int i = 0; i <= n; i++) {
queue<int> cc;
for(int j = 1; j <= n; j++) {
if(has[j])
continue;
if(cnt[j] <= i) {
cc.push(j);
has[j] = 1;
}
}
while(!cc.empty()) {
int v = cc.front();
owo.push(v);
cc.pop();
for(int u : edge[v]) {
if(has[u])
continue;
cnt[u]--;
if(cnt[u] <= i) {
cc.push(u);
has[u] = 1;
}
}
}
}
while(!owo.empty()) {
int v = owo.top();
owo.pop();
has[v] = 0;
for(int u : edge[v]) {
if(has[u])
continue;
uni(u, v);
rcnt[v]++;
}
ans = max(ans, rcnt[v] * sz[fnd(v)]);
}
cout << ans << '\n';
return 0;
}
|
