TIOJ-1606

發表於 更新於 Disqus：

你有一個長度 $n$ 的陣列 $arr$，一開始每項都是 $0$。

接著有 $q$ 筆操作，每筆操作可能是：

$1\ l\ r\ a\ b$：對於所有 $l\le i\le r$，$arr_i := a\times (i - l + 1)\mod b$。

$2\ l\ r$：詢問 $\sum_{i=l}^r arr_i$。

$n\le 10^9, q\le 5\times 10^4, a\le 10^6, b\le 10^6$

這題基本上動態開點會吃 TLE :(
所以先離散化。不難發現這個是個區間修改區間和的問題。
每個節點除了和以外，懶標的部份我們額外維護 $st, a, b$，代表這個節點的和是 $\sum_{i = 1}^{len} (a\times (i+st)\mod b)$，其中 $len$ 代表區間長度。這樣下推時就能很好的把這三個資訊給下推。

因此接下來的問題就是，給定了那三個資訊，有沒有辦法在夠快的時間內知道這個節點的和是多少？
首先令 $S(n)=\sum_{i=0}^n (a\times i\mod b)$，那這個節點的和會是 $S(st+len)-S(st)$，接下來我們把 $S(n)$ 給展開:
$$\begin{align*} S(n) &=\sum_{i=0}^n (a\times i\mod b) \\ &=\sum_{i=0}^n (a\times i - \lfloor \frac{a\times i}{b} \rfloor \times b) \\ &=\sum_{i=0}^n a\times i - \sum_{i=0}^n \lfloor \frac{a\times i}{b} \rfloor \times b \\ &= a\times \frac{n(n+1)}{2} + b\times \sum_{i=0}^n \lfloor \frac{a\times i}{b} \rfloor \end{align*}$$
於是問題就變成了怎麼計算最後那陀除法總和。
注意到如果 $a,b$ 不互質，那可以同除最大公因數來約分讓他們互質，所以我們以下考慮 $a, b$ 互質的情況。

如果 $a\geq b$，那 $\sum_{i=0}^n \lfloor \frac{ai}{b} \rfloor = \lfloor \frac ab \rfloor \times \frac{n(n+1)}{2} + \sum_{i=0}^n \lfloor \frac{(a\mod b)i}{b} \rfloor$，於是問題就變回 $a\lt b$了。

接下來考慮 $a\lt b$ 且 $a\neq 0$，其實 $\sum_{i=0}^n \lfloor \frac{ai}{b} \rfloor$ 可以看成在一個 $(0,0),(n,0),(n,\frac{an}b)$ 的三角形內部（含邊上）有多少個不在 x 軸上的格子點？

也就是下圖的藍色區域有多少格子點。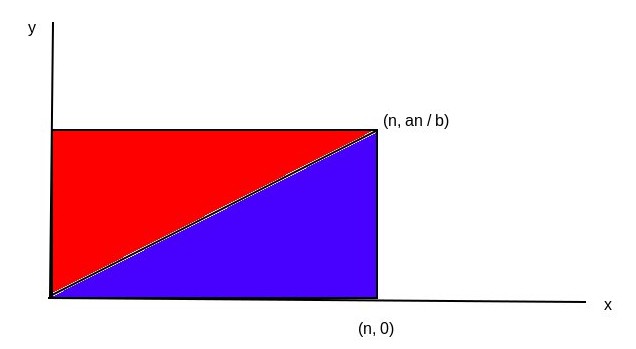
插圖
只不過藍色區域似乎不太好算？
可是整個矩形內部的格子點數量很好算！就是 $n\times \lfloor \frac{an}{b}\rfloor$！

而在對角線上的格子點數量呢？也很好算！因為 $a, b$ 互質，所以只有在 $i$ 是 $b$ 的倍數的時候 $\frac{ai}{b}$ 是整數。因此格子點數量就是 $\frac{n}{b}$。

因此只要我們會算紅色區域的格子點數量，那藍色區域就是（整個矩形）-（紅色區域）+（對角線上的格子點）了！

那要怎麼算紅色區域的格子點數量呢？你試著把頭往右轉 90 度看這張圖，你會發現其實他等同於這樣：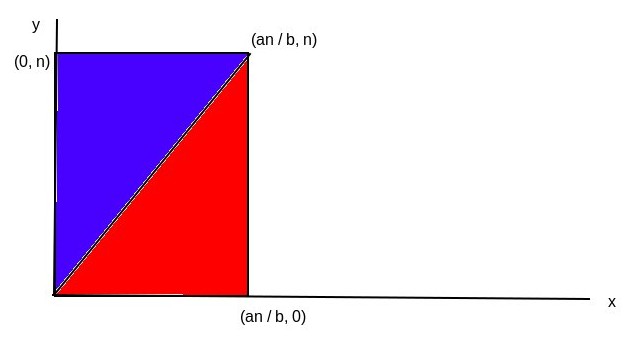
插圖2
於是紅色區域的格子點數量其實就是當 $a’=b, b’=a, n’=\lfloor \frac{an}{b} \rfloor$ 時的答案了！因為 $a’\gt b’$，所以會先回到第一個 case，並且取 mod 後再回到第二個 case，因為每次取 mod 都會造成 $a$ 或 $b$ 其中一個被砍掉至少一半，所以計算的過程會在 $\mathcal{O}(\log \max(a,b))$ 的時間內跑完！

配上線段樹的 $\mathcal{O}(n\log n)$，整體複雜度 $\mathcal{O}(n\log n\log \max(a, b))$。

實作的部份小心 overflow，不過因為最後輸出的答案會在 long long 範圍內，所以變數型態開 unsigned long long 就能當成在 $\mod 2^{64}$ 的情況下計算了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
/*
--------------              |   /
      |                     |  /
      |                     | /
      |             *       |/          |    |         ------            *
      |                     |           |    |        /      \
      |             |       |\          |    |       |       |\          |
   \  |             |       | \         |    |       |       | \         |
    \ |             |       |  \        |    |        \     /   \        |
     V              |       |   \        \__/|         -----     \       |
*/
#include <bits/stdc++.h>
using namespace std;

#define EmiliaMyWife ios::sync_with_stdio(0); cin.tie(NULL);
using ull = uint64_t;
const double EPS  = 1e-8;
static int Lamy_is_cute = []() {
	EmiliaMyWife
	return 48763;
}();
/*--------------------------------------------------------------------------------------*/

ull calc(ull a, ull b, int n) {
	ull k = a / b;
	ull extra = k * (1 + n) * n / 2;
	a %= b;

	if(a == 0)
		return extra;
	
	ull total = a * n / b * n;
	ull on_edge = n / b;

	return total - calc(b, a, a * n / b) + on_edge + extra;
}

inline ull cal(ull a, int b, int n) {
	ull g = __gcd(a, ull(b));
	return 1LL * (1 + n) * n / 2 * a - calc(a / g, b / g, n) * b;
}

vector<int> v;
const int N = 1e5 + 25;
struct segtree {
	struct node {
		ull v;
		// tag
		int fst = -1, a, b;
	} arr[N << 2];
	int n;
	void init(int _n) { n = _n; }
	void upd(int id, int fst, int len, int a, int b) {
		arr[id].fst = fst;
		arr[id].a = a;
		arr[id].b = b;
		arr[id].v = cal(a, b, fst + len) - cal(a, b, fst);
	}
	void push(int id, int l, int r) {
		if(arr[id].fst == -1)
			return;
		int m = l + r >> 1;
		upd(id << 1, arr[id].fst, v[m] - v[l], arr[id].a, arr[id].b);
		upd(id << 1 | 1, arr[id].fst + v[m] - v[l], v[r] - v[m], arr[id].a, arr[id].b);
		arr[id].fst = -1;
	}
	int edt(int id, int l, int r, int ql, int qr, int fst, int a, int b) {
		if(r <= ql || qr <= l)
			return 0;
		if(ql <= l && r <= qr) {
			upd(id, fst, v[r] - v[l], a, b);
			return v[r] - v[l];
		}
		push(id, l, r);
		int m = l + r >> 1;
		int w = edt(id << 1, l, m, ql, qr, fst, a, b);
		w += edt(id << 1 | 1, m, r, ql, qr, fst + w, a, b);
		arr[id].v = arr[id << 1].v + arr[id << 1 | 1].v;
		return w;
	}
	inline void edt(int l, int r, int a, int b) { edt(1, 0, n, l, r, 0, a, b); }
	ull que(int id, int l, int r, int ql, int qr) {
		if(r <= ql || qr <= l)
			return 0;
		if(ql <= l && r <= qr)
			return arr[id].v;
		push(id, l, r);
		int m = l + r >> 1;
		return que(id << 1, l, m, ql, qr) + que(id << 1 | 1, m, r, ql, qr);
	}
	inline ull que(int l, int r) { return que(1, 0, n, l, r); }
} tree;

signed main() {
	int n, q;
	cin >> n >> q;
	vector<tuple<int, int, int, int, int>> que(q);
	for(int i = 0, t, l, r, a, b; i < q; i++) {
		cin >> t >> l >> r;
		if(t == 1)
			cin >> a >> b, a %= b;
		l--;
		que[i] = {t, l, r, a, b};
		v.push_back(l);
		v.push_back(r);
	}
	sort(v.begin(), v.end());
	v.erase(unique(v.begin(), v.end()), v.end());

	tree.init(v.size());
	for(auto &[_, l, r, __, ___] : que) {
		l = lower_bound(v.begin(), v.end(), l) - v.begin();
		r = lower_bound(v.begin(), v.end(), r) - v.begin();
	}
	for(const auto &[t, l, r, a, b] : que) {
		if(t == 1)
			tree.edt(l, r, a, b);
		else
			cout << tree.que(l, r) << '\n';
	}
}